筹划了一段时间，终于开始写这个综述了。也算是做个总结吧。 这个综述将聚焦于基于 ReRAM 的存算一体的 DNN 加速器设计。

存算一体（ PIM ）

存算一体（ Process-in-Memory, PIM ； 也有称为 Compute-in-Memory 或 In-Memory-Computing 的，但都是一个东西）是一个比较“古老”的概念了。 在这里我们就简单定性地介绍一下这个 PIM ¹。

在介绍 PIM 之前要提一下冯$\cdot$诺依曼架构，也就是现在普遍应用的架构，的一个特点。 这个特点就是存储和计算单元是分离的。 也就是说在计算时要先将数据从存储器中读取到计算单元中，再由计算单元执行计算。 这样就会产生数据读写和搬移的功耗。 目前的大部分的 workload 都是计算密集（ CPU Bound ）的，即计算量远大于存储的读写量，因此体现不出这个数据搬移带来的开销的影响。 但是，随着深度神经网络（ Deep-Neural-Network ， DNN ）的崛起，情况开始变得不同了。 DNN 中存在大量的矩阵运算，而矩阵运算是存储密集的（ Memory Bound ），因此数据搬移的的开销就成为了一个问题。

PIM ，顾名思义，就是直接在存储器内执行计算。 这样就省去了数据搬移的开销。 目前我了解的 PIM 有如下几种路径：

1. 近存计算

   近存计算就是在存储器旁边直接放置计算电路。 这样数据就不用搬到计算单元中计算，就直接在存储器旁边计算。 这种方式实现非常简单，直接在 FPGA 上实现就可以。

2. 基于 SRAM 、 DRAM 等已知器件的存内计算

   这一类方法开发了这些存储器件的计算潜力。 比如，直接在字线上进行电荷共享²、逻辑计算^{3 4}，或在 cell 内执行多比特相乘⁵。

3. 基于新器件的存内计算

   这个方式是利用一些新兴的阻性器件构成的阵列来计算，其中就包括了本文的主角——ReRAM。 除了ReRAM之外，还有FeRAM、PCM等器件，它们的计算原理基本相同。 计算原理我们接下来会说。

基于 ReRAM 的存算一体电路计算原理

ReRAM 阵列其实加速的只是向量-矩阵乘法。 它的原理如下图所示：

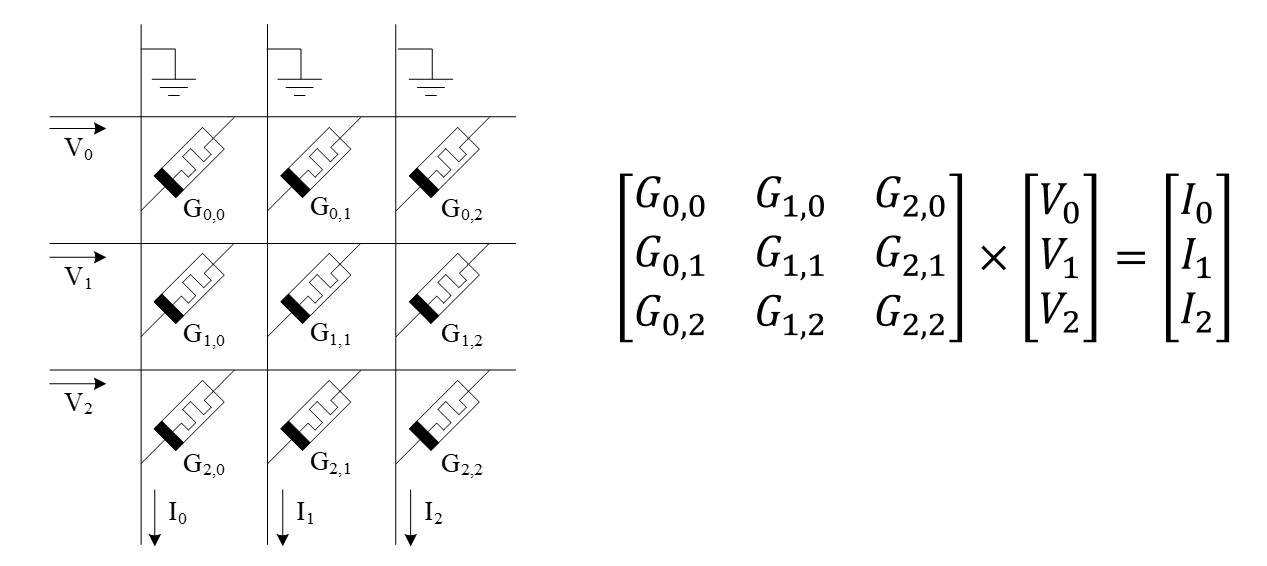
一列模拟电压信号输入到 ReRAM 阵列的 wordline 上，在每个 ReRAM 单元（ cell ）中，对应行的电压与 ReRAM 器件的电导相乘，得到一个小的模拟电路。 这个小的模拟电流在 bitline 上汇聚，并输出一行模拟电流信号。 这样，就完成了一个向量与一个矩阵的“乘累加”，即向量-矩阵相乘。 右面的公式表示了这个过程。 因此，要利用它进行计算，我们只需要将矩阵写在阵列上，再将向量以模拟电压的形式输入到 wordline 上，这样 bitline 上得到的结果就是计算结果。 这样，每个 ReRAM 单元都是一个乘法器，面积只有一个晶体管的大小（因为 ReRAM 是在金属层，可以直接做在晶体管上面，几乎不占面积），这比乘法器省了很多的面积。 同时 bitline 作用等同于一个组加法器树，将同一列的结果加起来，这与加法器相比面积也小得多。 总得来说，$28\mathrm{nm}$ 工艺下一个 $128\times128$ 的阵列的面积仅有 $25\mathrm{\mu m^2}$ ⁶，可以算一下它的面积效率，再和 V100 GPU比较一下（15.7$\mathrm{TFLOPS}$, 815$\mathrm{mm^2}$），就能知道它的潜力有多大了。

但是，在实际使用的过程中，这个东西完全没我们想象的那么好，主要是如下的几点理由。

1. 这个阵列完全是模拟计算，而我们的计算机中存储和传输的数据都是数字形式的，进一步地，是二进制的。
2. 受 ReRAM 工艺的限制，每个 ReRAM 单元只能写有限个比特，比如，2比特。我见过的最高的文章有能写6-8比特的，但我并不太相信。 这就导致了低精度的问题。

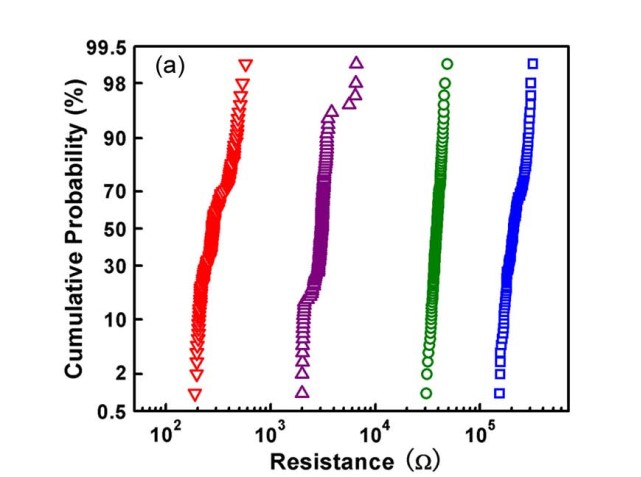
这里详细讨论一下为什么这个比特数会有限制。 这是因为 ReRAM 写有限的比特是因为它本身的阻值是写不准的，写上去的和期望的值有一个偏移（ Variation ），这个偏移有可能会导致相邻的两个阻态间有重叠。 比如下面那张图。 在下图这种情况下如果我们写四种电阻，那么我们很容易画三条竖线将这四种阻态分开，如果我们增加阻态个数，在$10^3$那里再“强行”塞入一个阻态，那个这个阻态就会和红色或紫色的阻态间重叠，被判决成这两种阻态，就不正确了。 这还是一个电阻的情况。 如果我们是$128\times128$这么大的阵列一列的电流相加，那么根据概率论知识，每个累积概率的线都会被横向拉伸，每个状态间更容易重叠。

由于这两个原因，我们就需要一些周边电路来支持它来实现我们期望的高精度的矩阵乘法。

基于 ReRAM 的存算一体的周边电路

数-模/模-数转换电路

为了解决问题一，我们要引入两个电路————模-数转换器（ Analog-to-Digital Converter ， ADC ）和数-模转换器（ Digital-to-Analog Converter ， DAC ）————作为 ReRAM 阵列内的模拟域和外部数字域间的“桥梁”。

但这两个电路仍面临很严重的精度问题。 首先，如果我们想要实现一个16比特的计算，我们就需要一个16-比特的DAC，这个东西并做不出来。 其次， DAC 和 ADC 的精度间是耦合的，这导致了功耗与精度的取舍问题。 就算我们只算4比特的计算， 4 比特的 DAC 有 16 种电平， 4 比特的 ReRAM 每个单元也有 16 种电阻，这一乘就是 256 种电流输出。 再加上同一列的 128 个 cell 输出电流的汇聚，就是 $2^{15}$ 种电流。 我们需要一个 15 比特的 ADC 来量化这个模拟电流。 且不说这么高比特的 ADC 能不能做出来，就算能做出来，想想 ADC 的功耗和分辨率可是成指数关系 ⁷，这么高比特的 ADC 功耗也是难以接受的。 这就限制了我们必需用低比特的 DAC ，每个 ReRAM 单元上写更少的比特。

S&H 电路

ADC 的频率可以远快于 ReRAM 阵列的计算速度，但面积比较大。 因此我们可以选择在 bitline 间共享 ADC 。 这就需要暂存模拟信号，我们可以用一种叫采样-保持（ Sample-and-Hold ， S&H ）的电路 ⁸ 实现这个功能。 这个电路实际上就是一个电容，存储一下电平，之后再将这个电平读出来。

bit-slice 方法和移加电路

为了 ADC 、 DAC 和问题二共同导致的精度问题，我们要引入 bit-slice 技术。 这个技术的目标是将多个低比特的向量-矩阵乘组合成一个高精度的向量-矩阵乘。 这个技术分两步，如下图所示：

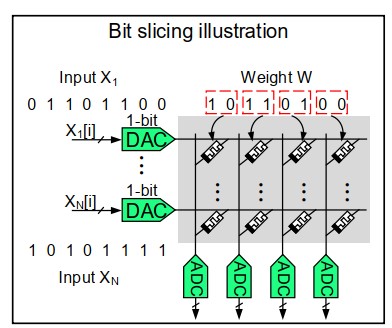
首先，对于 ReRAM 单元的精度问题，我们将原本设计中的 ReRAM 阵列的一列代表矩阵的一列，变成用相邻的多列来代表矩阵的一列。 将矩阵的每个数按比特由高到低从左到右写在这相邻的列上。 假设我们的阵列每个 cell 是 2 个比特，那么图中写一个 8 比特的数就要 4 列。 ReRAM 阵列的每一列完成对应位的乘累加后，我们将这些列的结果移位相加即可。

之后，对于 DAC 的精度问题，我们将输入的多个比特分周期依次从 DAC 输入进去。 假设我们的 DAC 分辨率为 1 比特，那么我们如果要输入一个 8 比特的输入，就需要 8 个周期。 在这之后，我们同样将结果移位相加即可。

这两个过程或许用数学公式会更好理解。 假设每个 ReRAM 单元可以写 $R_c$ 比特， DAC 的分辨率分别为 $R_{DAC}$ ，如果我们要计算一个 16 比特的乘法（矩阵 $A$ 和向量 $b$ 均为 16 比特），那么我们就要对这两个操作数进行 bit-slice ：

其中， $A_i$ 和 $b_i$ 均代表一个 slice 。 那么，我们的高比特乘法就可以写为：

可以看到，这两个步骤我们都需要对结果进行移位相加，因此我们需要引入一个数字的移位-相加器（ Shift-and-Add ， S+A ）来实现这个功能。

基于 ReRAM 阵列的向量-矩阵乘法器

综合我们以上的分析，再加上一些 I/OR （ Input/Output Register ），就可以得到一个典型的 ReRAM 矩阵乘法器的结构图了。

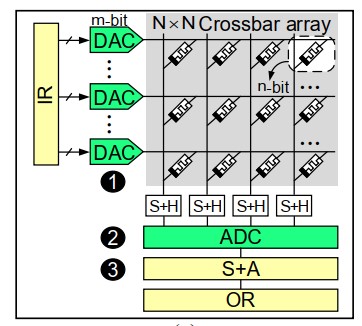
总结

本文从原理上介绍了 ReRAM 阵列的计算原理以及一个基础的周边电路设置。 在接下来的章节中我们将介绍几个完整的架构设计。

下一章链接： 基于 ReRAM 的神经网络加速器综述（二）——早期的加速器